“Time for homework! 📚” - I read the notification on the top left of my field of vision. I close the simulation of the remotely controlled pirate ship I was crafting. I put down my haptic gloves on my bed, and turn off the 3D hologram projector.
I turn to the other side of my room and open the blackboard. With a piece of chalk, I write the math assignment for today.
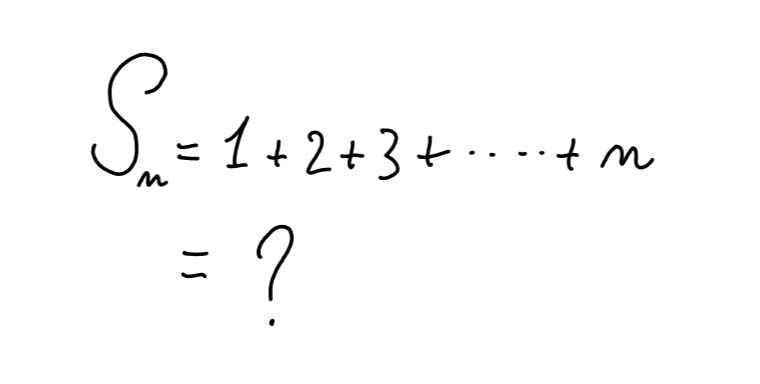
I begin by using the sigma notation the professor introduced today in the first course about sums.
As I was tracing the last letter, a blue stroke quickly barred what I just wrote. “Unnecessary!” the blackboard adds.
“Okay, okay,” I think to myself, frustrated while I erase the line, “Sorry for trying to apply what I just learned.”
I take a step back and ponder, staring at the empty space following the equal sign. Nothing comes up. I have no idea on how to go about this one; my brain is blank.
After thinking for about thirty seconds, the fluid blue stroke reappears. It starts moving along long and straight lines, and followed by a grid made of dotted lines that appear like a rain of geometrically organized droplets coming from the other side of the blackboard.
I look at the empty grid, confused. I was expecting some sort of clever symbol manipulation of the sort we saw in class today, not a geometry puzzle!
The blackboard picks up on my desperate face, and quickly proceeds to complete the drawing. In a slow movement, it fills the bottom right square of the grid with diagonal lines, and finishes by writing in a careful handwriting, “1.”
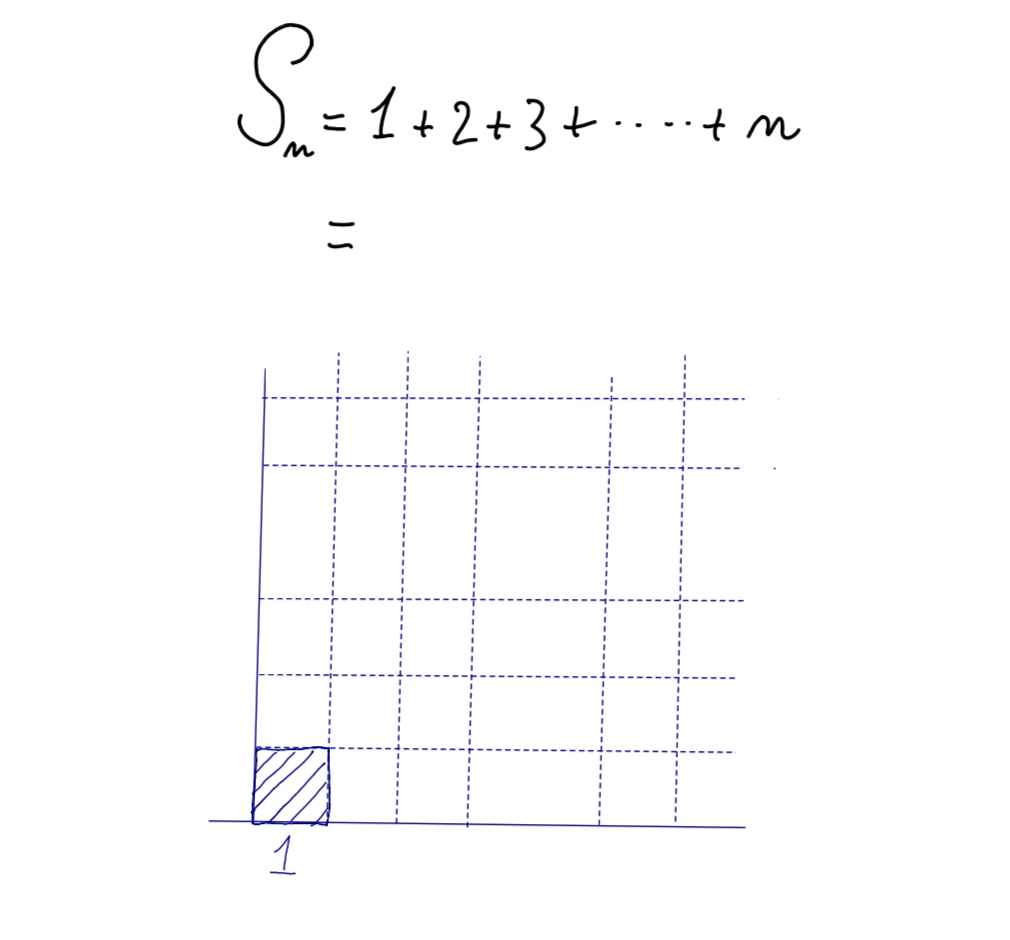
This time, the stroke is thinner; it prompts me to write on top of it, as if reproducing the movement will give me access to the intention of the blackboard.
I was about to lift the chalk from the board when the faint line reappeared, to carefully add a “2” near the “1.”
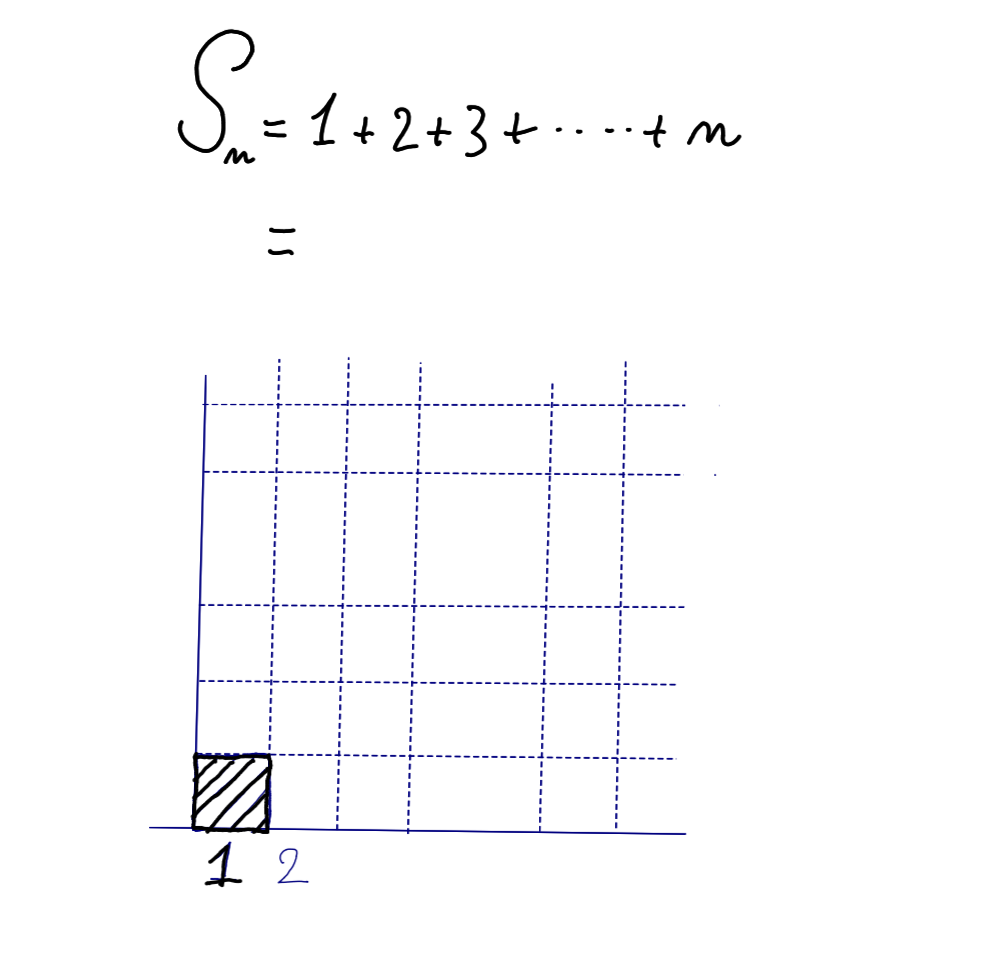
I continue the pattern by filling a rectangle of height 2 above the number. I stop, waiting for further hints. But all I receive is a quick succession of three dots, impatient for me to continue the sequence.
“Yeah! I got you, don’t worry,” I say to myself as I finish filling the rectangles and their corresponding indices.
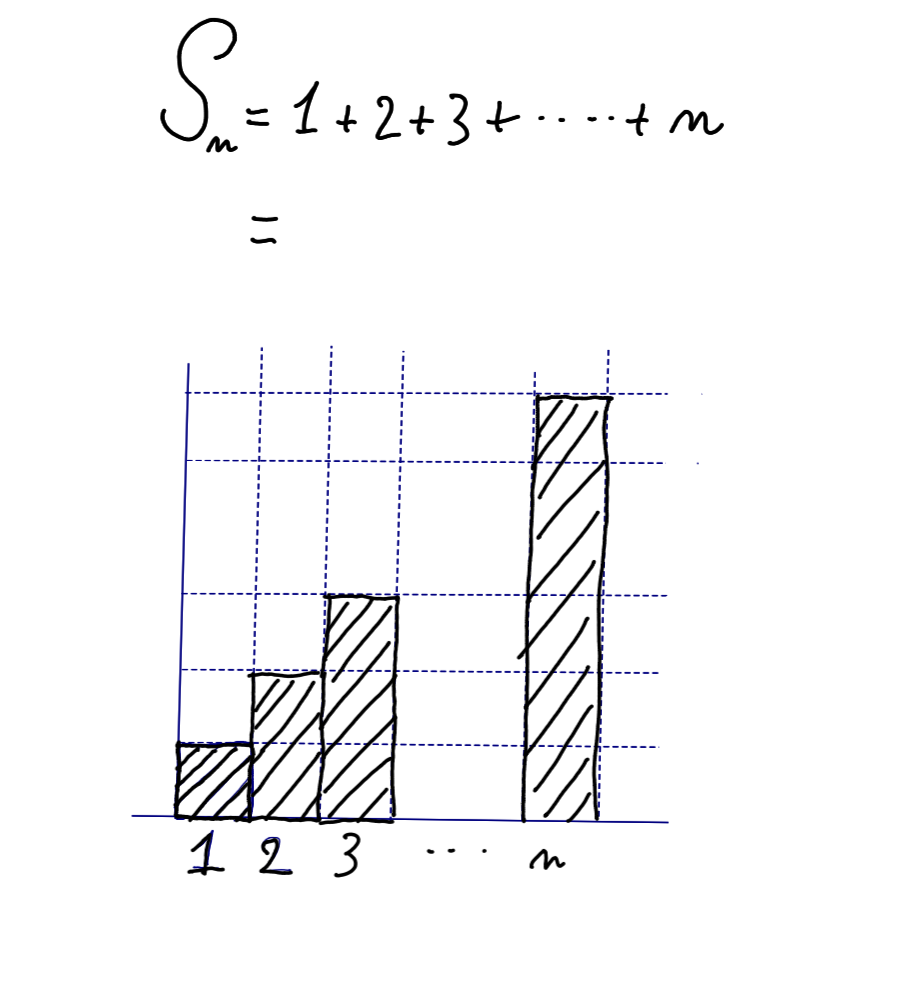
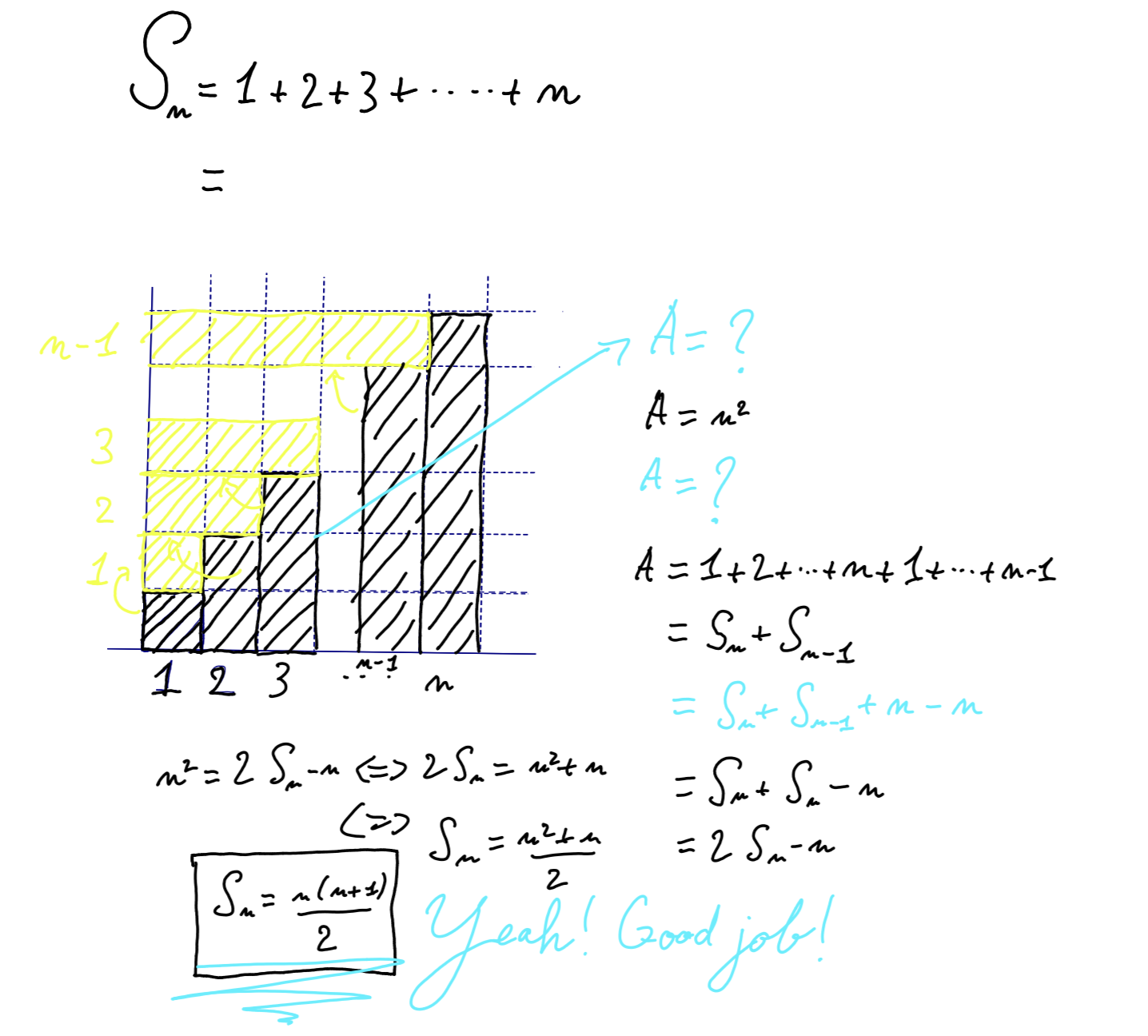
I now understand what the blackboard wants me to do: computing the sum is the same as counting how many squares you can fit in the barred shape. It transformed the problem of computing a sum into a problem of measuring an area.
I look at the blackboard for a minute or two. The blackboard stays silent. It expects me to take the lead. It knows my level, and its quietness means that it evaluates that I’m able to find where to go from there.
If I keep waiting, I can only expect it to write kind words to cheer me up, clarifying answers, or suggesting I come back to the problem after some rest. It guided me up to this point, and it will not give away the answer; it has to come from me.
After looking at the stair-like shape for 5 minutes, it starts to feel like a word repeated 20 times, a sound that has lost its meaning. I’ve seen too much of it.
I start to loose focus; my eyes wander around, are drawn to my haptic gloves on the bed. I look at the mountain cliffs I can see afar from my window.
I turn back to the blackboard, my mind lingering. The staircase shape grabs my eyes; I look at it intensely, trying to read some kind of obfuscated truth hidden in the grid.
Then, my mind half-wandering, I am attracted to the holes of the grid, the negative of the filled rectangles. I play with the bars in my head; I take the vertical bars, rotate them, and stick them horizontally. I grab a yellow chalk to draw this transformation; the shapes neatly fit together. I add their corresponding numbers on the vertical axis, and stop at n-1: reporting the last bar would get me outside of the grid.
The blackboard awakens from its silence to reward me with a cheerful “Nice intuition!”.
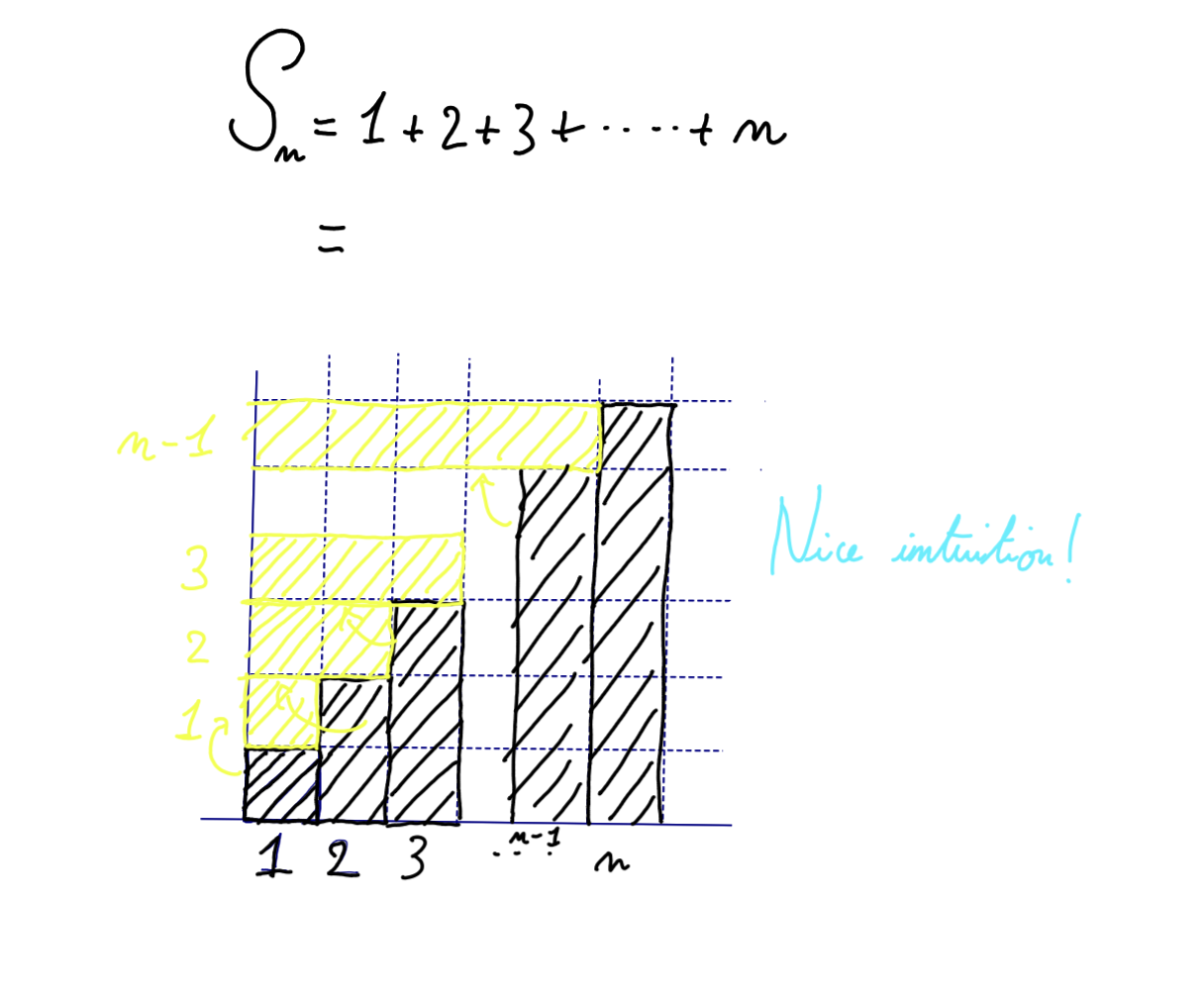
It goes on to draw an arrow from the grid, and asks, \(A = ?\).
\(A = n²\), I write, giving the area of the large square. \(A = ?\), the blackboard repeats below. “I just computed it!” - I think aloud, frustrated. After a quick pause, I understand what it is asking for: a second way to express the same area.
\[\begin{align*} A &= 1 + 2 + ... + n + 1 + 2 + ... + n-1 \\ &= S_{n} + S_{n-1} \end{align*}\]I write, summing up the yellow and black numbers indicating the area of each rectangle filling the square.
\(= S_{n} + S_{n-1} + n - n\), the blackboard continues.
Yes! I remember this plus minus trick! It adds up to zero, but introduce useful quantity to combine symbols with. Here I recognize that \(S_{n-1} + n = S_{n}\).
\(= 2S_{n} - n \) I proudly write. I continue with a growing excitement as I feel the solution is at my fingertips. From there, only straightforward symbol manipulation are left to solve an equation with a single unknown.
I draw a box around the final result. As I’m tracing the final side of the box, the blackboard draws with me an enthusiastic zigzag complemented by a “Yeah! Good job!”.